
 |
PUZZLE |
Calcudoku Puzzle Rules
The rules of Calcudoku Puzzles are as follows:
Here is an image of the start position of a Calcudoku puzzle:
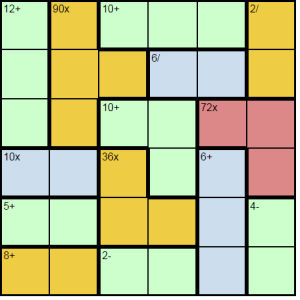
There is a lot to digest in the rules above. First, it is worth pointing out that it is unusual in a sudoku variant for repetition to be allowed, and it is important to bear this in mind. That's particularly true if you are used to playing killer sudoku puzzles, which calcudoku builds upon by also introducing subtraction, division and multiplication, since in killer sudoku numbers cannot repeat within sum regions.
Look at the 36x yellow region in the bottom-middle of the image above. Due to repetition being allowed, and the shape of the region, the values could be 6,1,6. However, if the 36x region was in a straight vertical line, then that wouldn't be possible, as then having 6,1,6 would mean the repetition of a number in a column, which is against the rules. It can take a little bit of getting used to.
The other thing to point out that can confuse is the way that the subtraction and division regions work, as outlined above. The addition and multiplication is easy: that's because 2+3 is the same as 3+2, and 2x3 is the same as 3x2. However, that's clearly not the case with subtraction and division: 2-3 is not the same as 3-2 and 3/2 is not the same as 2/3 (note that the puzzles use / to indicate division).
In other words, with subtraction and division, order matters. Therefore it's key to bear in mind that you must find the highest number in each division and subtraction region, and subtract from that number, or divide it by the other numbers, as relevant. Thus, the 4- in the bottom right of the example grid above must contain 6 and 2 or 5 and 1 in some order. But it doesn't matter whether the actual order is 2,6 or 6,2 or 5,1 or 1,5 since the rule is, as explained, however they are actually arranged, you perform the calculation in the specified order.
If you would like a visual explanation of the rules of calcudoku, here is a video that explains the rules:
Play A Sample Calcudoku Puzzle
If you'd like to have a go at solving the Calcudoku puzzle shown above now that you know the rules of the game, you can play via our Online Calcudoku Puzzle Player
Once you have solved the puzzle if you tried it (or got stuck and want to see how to solve it), then you might also find the video below interesting, that walks through how to solve the puzzle:
If you enjoy this puzzle type, you can join our online Puzzle Connoisseur's Club for £12 or $17 a year and play a new Calcudoku Puzzle puzzle every day of the year, together with many other fun and interesting logic puzzles.
Strategy and Solving Tips for Calcudoku Puzzles
The video above walks through the solve of the sample puzzle, and in so doing reveals some of the logic that can be used to solve calcudoku puzzles. It's important to note that all our calcudoku puzzles can be solved using logic alone, and no guessing is ever required to reach the single solution. Here are a few strategy tips: